网络,是由节点(nodes)和链接(edges)所组成。节点(node),其他领域可能会用行动者(actors)或是顶点(vertex)来称呼,节点可以代表个人、产品、事件、国家。链接(edge),是代表节点之间的关系,在其他领域会用弧线(arc)或是连接(link)来称呼,链接可以代表个人共同喜欢的物件、个人共同著作等关系。

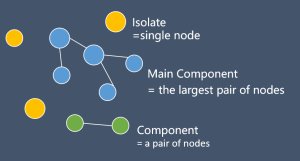
在网络图中,单一节点如下图黄点(single node)英文又称isolate,一组节点(a pair of nodes)英文又称component,网络中最大组节点(the largest pair of nodes),称main component。
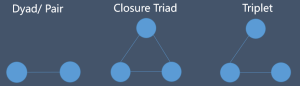
一组节点可称为pair或是dyad(下图左),三个节点链接成封闭三角可称为closure triad(下图中),三节点链接开放三角则称triplet(下图右)。
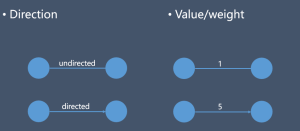
节点和节点之间的链接可以分为无方向性(undirected)、有方向性(directed),链接的次数亦可以计算,例如:连接5次,则链接权重(edge weight; value)是5。
接来用说明有向和无向网络图的差异(为有助于理解,以下中英文并用)。
Graph G
=a finite set of nodes, N (each node is unique)
+a finite set of edges, E (each edge is unique)
Each edge is a pair (n1,n2) where n1, n2 ∈ N
假设图G包含:一组有限量的节点N和一组有限量的链接E,且每一节点与每一链接都是唯一的,节点以n1、n2表示,链接以(n1,n2)表示。
【无向图(undirected)】网络图
N = { 1, 2 ,3, 4, 5}
E = { (1,2), (1, 5) , (2, 3), (2, 4), (3, 4), (4, 5), (2,1), (3, 2), (4, 2), (4, 3), (5, 1) (5, 4)}
All edges are two-way. Edges are unordered pairs.
可以看出有5个节点,6条链接,链接是双向的、是没有次序的,矩阵可以写成下图右边的形式,无像图的矩阵数值会沿著对角线对称。

【有向图(directed)】 网络图
N = { 1, 2, 3, 4, 5}
E = { (1, 2), (1, 5), (2, 3), (3, 4), (4, 2), (4, 5), (5, 1) }
All edges are one-way as indicated by the arrows. Edges are ordered pairs.
可以看出有5个节点,6条有箭头的链接,链接是单向的、是有次序的,矩阵可以写成下图右边的形式。

【有向图+权重】网络图
N = { 1, 2, 3, 4, 5}
E = { (1, 2), (1, 5), (2, 3), (3, 4), (4, 2), (4, 5), (5, 1) }
All edges are one-way as indicated by the arrows. Edges are ordered pairs.
可以看出有5个节点,6条有箭头的链接,链接是单向的、是有次序的,加上链接权重的概念,可以知道(1,5)的链接数是3;(4,2)的链接数是6;(5,1)的链接数是7,矩阵可以写成下图右边的形式。

其他专有名词:

by范蔚敏